| Nasa ParaWing |  |
| Nasa ParaWing |  |
|
|
| Here is the "heart" of excel spreadsheet,
just a few maths formulas, don't be afraid ! |
 |
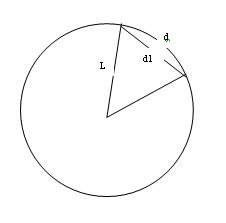
details on profile computation
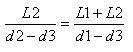
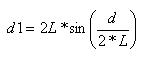  |
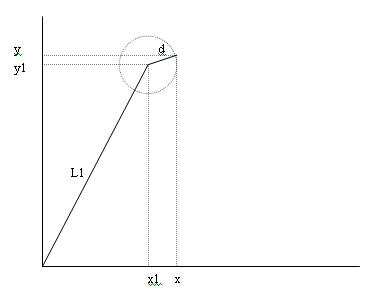
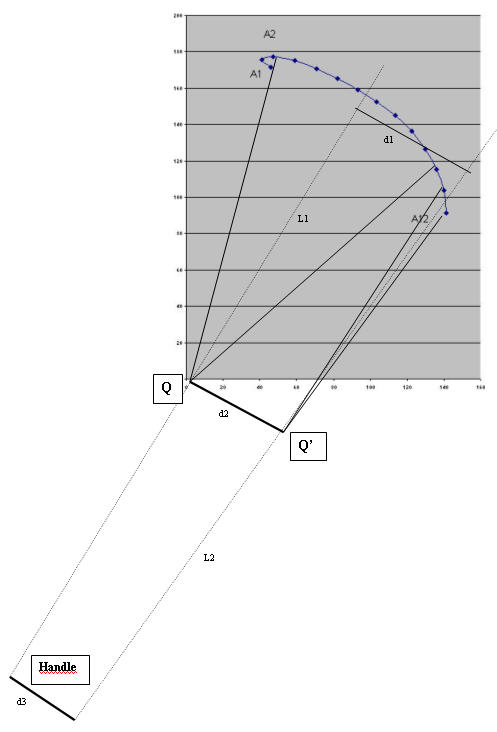 |
if we notice that we get |
 |
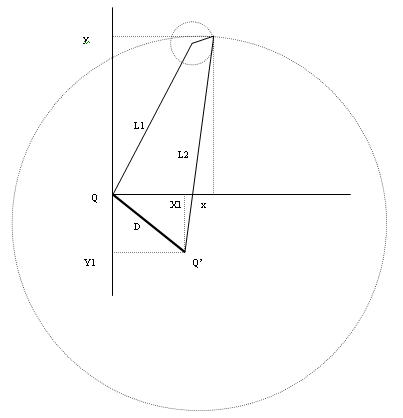
Note that if we choose D = 0 then Q’ point is equal to Q point. This
means that L2 line is NOT a brake line. So the same formula can be used
both for brakes and not brake lines !
Equation of this circle is given by formula (2) we get 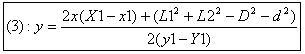
(4) can be writen in the usual form where the only « unknown » is x the solution (we only keep the greatest x value) is
|
|
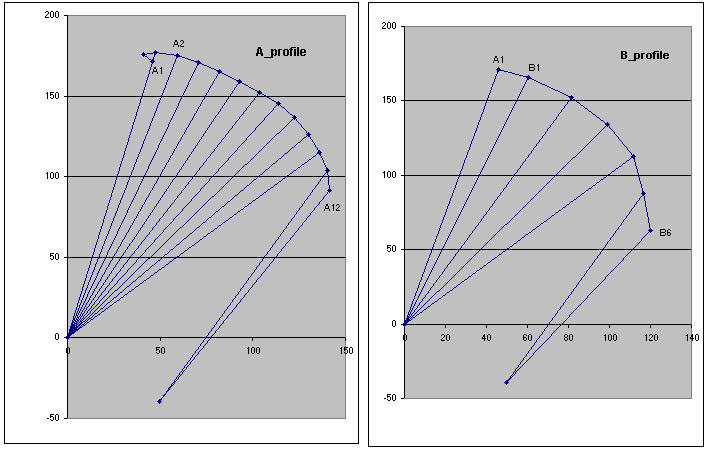
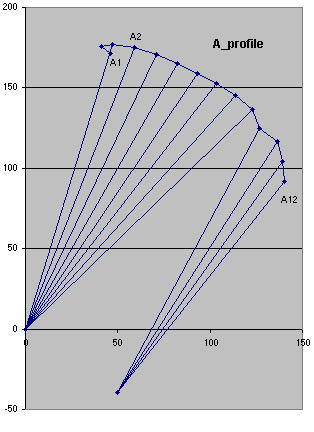
| You can modify some parameters of the excel spreadsheet to draw your
own profiles
here are accessibles parameters :
|
 |
|
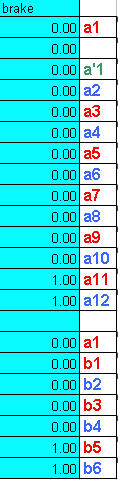 |
here I have intentionnaly put a brake on A9 to A12 lines without modifying bridles lengths
|
 |